Chapter2. Perceptron(퍼셉트론)

2.1 퍼셉트론이란?

• Perceptron (퍼셉트론) : 신경망(딥러닝)의 기원이 되는 알고리즘
• 1 : 신호가 흐른다. / 0 : 신호가 흐르지 않는다 

$x_1$, $x_2$ : 입력신호

$y$ : 출력신호

$w_1$, $w_2$ : 가중치

○ : 뉴런 또는 노드

 

-> 뉴런에서 보내온 신호의 총합이 정해진 한계인

임계값 ($\theta$, 세타)를 넘어설 때만 1을 출력

$y=\{\begin{array}{ll}0& w_1{x}_1+w_2{x}_2\le \theta \\ 1& w_1{x}_1+w_2{x}_2>\theta \end{array}$

2.2 단순한 논리회로

2.3 퍼셉트론 구현하기

2.3.1 간단히 구현하기

1) AND 구현하기

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1 * w1 + x2 * w2
    if tmp > theta:
    	return 1
    elif tmp <= theta:
    	return 0

2) NAND 구현하기

def NAND(x1, x2):
    if AND(x1, x2)==0:
    	return 1
    elif AND(x1, x2)==1:
    	return 0

3) OR 구현하기

def OR(x1, x2):
    w1,w2,theta=0.5,0.5, 0
    tmp = x1 * w1 + x2 * w2
    if tmp > theta:
      return 1
    elif tmp<=theta:
      return 0

2.3.2 가중치와 편향 도입

$\theta$=-$b$로 치환

=>$y=\{\begin{array}{ll}b+x_1{w}_1+x_2{w}_2\le 0이면& 0\\ b+x_1{w}_1+x_2{w}_2>0이면& 1\end{array}$

 

가중치 ($w$) : 입력신호가 결과에 주는 영향력(중요도)를 조절하는 매개 변수

편향 ($b$) :  뉴런이 얼마나 쉽게 활성화 하느냐를 조정하는 매개 변수

2.3.3 가중치와 편향 구현하기

1) AND구현하기

import numpy as np

def AND(x1, x2):
  x= np.array([x1,x2])
  w= np.array([0.5 ,0.5])
  b=-0.7

  tmp=np.sum(x*w)+b
  if tmp <=0:
    return 0
  else:
    return 1

2) NAND 구현하기

def NAND(x1,x2):
  x= np.array([x1,x2])
  w= np.array([-0.5 ,-0.5])
  b=0.7

  tmp=np.sum(x*w)+b
  if tmp <=0:
    return 0
  else:
    return 1

3) OR 구현하기

def OR(x1, x2):
  x= np.array([x1,x2])
  w= np.array([0.5,0.5])
  b =-0.2
  tmp= np.sum(x*w)+b
  if tmp <=0:
    return 0
  else:
    return 1

2.4 퍼셉트론의 한계

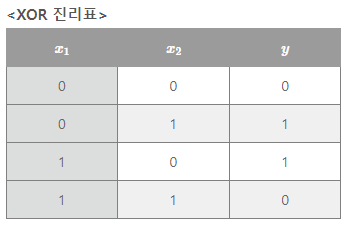
XOR 게이트 , 비선형

XOR 게이트는 배타적 논리합이라는 논리 회로이다. 즉. $x_1$과 $x_2$중 한쪽이 1일 때만 1을 출력한다.

여기서 배타적은 자기 외에는 거부한다는 의미이다.

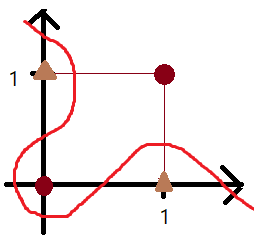
위의 오른쪽 그림은 $x$축은 $x_1$이고 y축은 $x_2$이고 동그라미는 $y$가 0인 경우, 세모는 $y$가 0인 경우이다.

동그라미와 세모를 분류하려면 AND나 OR같이 한직선으로 되지 않는 것을 볼 수 있다. 두 분류를 나타내려면 두 직선이거나 왼쪽 그림과 같이 곡선의 형태여야된다.

따라서, AND나 OR 처럼 직선의 영역을 선형영역이고 XOR은 곡선의 영역을 비선형 영역이라 한다.

 

 

2.5 다층 퍼셉트론(Multi-layer perceptron)이 출동한다면 

2.5.1 기존 게이트 조합하기

위의 게이트 기호로 XOR게이트를 표현해보자. NAND와 OR의 출력이 AND게이트로 통과하여 출력하면 XOR 게이트와 같은 결과가 나온다 . 오른쪽 진리표를 보면 S1은 NAND결과이고 S2는 OR의 결과이다. 이 둘의 결과를 AND게이트를 통과하여 y가 출력이 되는데 이 결과는 XOR게이트 통과한 결과와 같다. 위의 게이트 기호로 표현하면 아래의 그림과 같다.

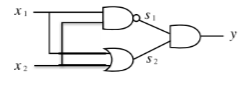
2.5.2 XOR 게이트 구현하기

def XOR(x1, x2):
	s1 = OR(x1, x2)
	s2 = NAND(x1, x2)
	y = AND(s1, s2)
	if y > 0:
		return 1
	else:
		return 0

지금 구현한 XOR를 뉴런을 이용한 퍼셉트론으로 표현하면 밑의 그림처럼 표현됩니다.

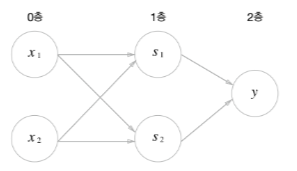
<뉴런 동작 순서>

1. 0층의 두 뉴런이 입력신호를 받아 1층의 뉴런으로 신호를 보낸다.

2. 1층의 뉴런이 2층의 뉴런으로 신호를 보내고 2층의 뉴런은 y를 출력한다.

 

※ 그림은 모두 3층으로 구성됩니다. 그러나 가중치를 갖는 층은 2개(0층과 1층 사이, 1층과 2층 사이)뿐이여서 '2층 퍼셉트론'이라 부릅니다. 기준에 따라 '3층 퍼셉트론'이라 하는 경우도 있습니다.