| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- join
- sqlite3
- Depthwise Convolution
- 미니배치
- 학습 구현
- 합계
- sigmoid
- 평균
- Pointwise Convolution
- 렐루함수
- 시험데이터
- PYTHON
- max
- 신경망
- total
- next.js 튜토리얼
- 교차엔트로피오차
- 수치미분
- 최댓값
- Next.js
- Depthwise Separagle Convolution
- 데이터베이스
- 오차제곱합
- 밑바닥부터 시작하는 딥러닝
- AVG
- sum
- 제약조건
- COUNT
- MIN
- PyQt5
- Today
- Total
우잉's Development
Cross-Entropy 본문
1. Logistic Classification
: 분류 문제가 주어질 때 사용하고 특히 둘 중 하나를 선택하는 binary의 경우 사용
binary 한 문제의 경우 결과 값이 0 또는 1이면 충분하지만 선형 회귀 모델을 입력에 따라 예측값이 선형적으로
증가하므로 크게 나올 수 있다. 말로 설명하면 어려우므로 예를 들어보겠습니다.
예) 시간에 따른 시험 합격 or 불합격 예측
2, 3, 4시간 공부할 경우 FAIL 5, 6, 7시간 공부할 때 PASS 한다고 하자. 그럼 아래와 같은 그래프가 나온다.
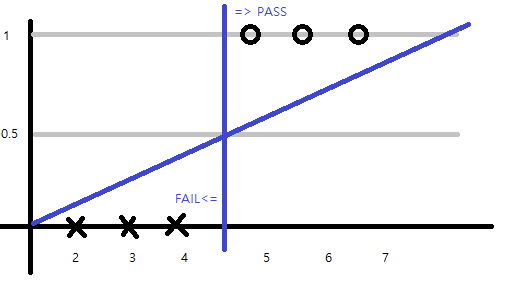
Y값이 0.5를 기준으로 오른쪽은 PASS, 왼쪽은 FAIL이 나올 것이다.
만약 5시간 공부하면 결과값으로 PASS가 나올 것이다. 이걸 다시 학습시키면 그래프는 어떤 변화가 있을까?

위 그림과 같이 그래프는 더 낮은 기울기를 가지고 0.5 기준으로 나눈 PASS 또는 FAIL의 시간 기준이 변경이 된다.
따라서 5시간 공부할 때 결과 값은 PASS지만 여기서는 FAIL이라는 잘못된 결과 값을 가져온다.
이런 경우에 0~1 사이의 값으로 정규화 해준다. 이때 사용하는 특별한 함수를 sigmoid function(logistic function)이라
부른다.

\(H(X) = {1 \over {1+e^{-W^T X}}}\)
2. logistic classification의 cost function
- cost function : 실제값과 예측값의 차이를 나타내는 함수
선형 회귀 모델과 동일한 함수를 사용하는 logistic classification은 위에서 알게 된 sigmoid함수를 적용한다면 손실 함수
가 최소인 값을 미분을 이용해 구하기 어려워진다. 왜냐하면 아래와 같이 울퉁불퉁한 형태로 그래프가 그려지기 때문이다.
<local minimum & Global minimum>

\(cost(W) = {1\over m} \sum c(H(x), y)\)
\(c(H(x), y) = \begin{cases} - log(H(x)) & if &y=1 \\ -log(1-H(x)) & if& y=0 \end{cases} \)
위의 c함수를 그래프로 나타내면 아래와 같다.

\(y\)가 1일 경우와 \(y\)가 0일 경우는 서로 반대방향이다.
이 두 개의 식을 한 번에 표현하는 식은 아래와 같다.
\(c(H(x), y) = ylog(H(x))-(1-y)log(1-H(x)) \)
마지막으로 목적이 손실이 최소가 되는 최적의 W값을 구하기
위해 손실 함수를 W에 대해 미분함으로 쉽게 구할 수 있다.
\(W :=W-\alpha \frac{\partial }{\partial W} cost(W) \)
3. Multinomial classification
위에서는 binary 한 경우를 다뤘다면 이번에는 여러 개를 분류하는 경우를 살펴봅시다.
만약 세 가지 경우의 수를 비교한다 했을 경우, 로지스특회귀로도 세가지 경우를 예측 가능합니다.
이진 분류로 아래와 같이 나눠봅시다.

1) A인 경우 & A가 아닌 경우
2) B인 경우 & B가 아닌 경우
3) C인 경우 & C가 아닌 경우
이를 식으로 나타내면, 행렬곱으로 나타낼 수 있고
각각의 경우에는 예측값을 시그모이드 함수를 거쳐 1 혹은 0으로
나타내면 여러 개의 경우의 수도 분류 가능합니다.
이를 Multinomial classification입니다.
하지만, 다항 분류에서는 softmax가 사용됩니다.
4. Softmax function
\(softmax(x) = {e^x_i \over \sum_{j=0}^k e^x_j} (i=0, 1, ... k)\)

이 softmax함수를 사용하면, 각각의 경우의 수가 0~1 사이의 숫자로
그 경우의 수 총합이 1이 되도록 결괏값이 나오게 됩니다.
왼쪽 그림과 같이 모든 경우의 수 합이 1이면서, 각각의 경우의 수가
0~1 사이의 수로 나오게 되는 것입니다.
softmax함수를 거쳐 나온 결과를 One-Hot Encoding기법을 통해 [1, 0, 0]으로 나타낼 수 있습니다.
One-Hot Encoding기법은 해당 부분을 1로 표현하고 나머지는 0으로 표현하는 기법입니다. 여기서는 가장 큰 수를 1로
나머지를 0으로 나타내게 됩니다.
5. Cross Entropy
softmax 함수처럼 multimial인 경우의 손실을 최소화(최적화) 하기 위해서 사용되는 함수를 Cross Entropy라 합니다.
Cross Entropy는 다음과 같습니다.
\( CE = - \sum_i^C t_i log(f(x_i))\)
\(t_i\) : softmax에서 one-hot encoding 한 값 (컴퓨터가 예측한 값)
\(x_i\) : softmax함수를 거친 값 (실제 데이터의 값)
위 softmax에서 case를 세 가지로 나눠서 예를 들어서 이번에도 이용해서 진행하겠습니다.
case1 => A, case 2 => B, case 3 => C로 변경해서 행렬로 나타내면 \( \begin{bmatrix} A\\B\\C \end{bmatrix}\)입니다. 따라서 아래와 같이 A, B, C를 표현합니다.
case1 = A =\( \begin{bmatrix} 1\\0\\0 \end{bmatrix}\), case2 = B =\( \begin{bmatrix} 0\\1\\0 \end{bmatrix}\), case3 = C =\( \begin{bmatrix} 0\\0\\1 \end{bmatrix}\) 으로 나타냅니다.

Cross Entropy함수에 적용하면 다음과 같습니다.
A : \( \begin{bmatrix} 1\\0\\0 \end{bmatrix} \bigodot -log \begin{bmatrix} 1\\0\\0 \end{bmatrix} = \begin{bmatrix} 1\\0\\0 \end{bmatrix} \bigodot \begin{bmatrix} 0\\\infty\\\infty \end{bmatrix}\) = 0
B : \( \begin{bmatrix} 1\\0\\0 \end{bmatrix} \bigodot -log \begin{bmatrix} 0\\1\\0 \end{bmatrix} = \begin{bmatrix} 1\\0\\0 \end{bmatrix} \bigodot \begin{bmatrix} \infty\\0\\\infty \end{bmatrix}= \infty \)
C : \( \begin{bmatrix} 1\\0\\0 \end{bmatrix} \bigodot -log \begin{bmatrix} 0\\0\\1 \end{bmatrix} = \begin{bmatrix} 1\\0\\0 \end{bmatrix} \bigodot \begin{bmatrix} \infty\\\infty\\0 \end{bmatrix}= \infty \)
cross entropy는 크게 되면 예측이 틀린 것을 나타내고 작으면 예측이 맞게 됩니다.
'Deep learning > 용어 정리' 카테고리의 다른 글
| Local minima (0) | 2022.01.18 |
|---|---|
| Binary Cross Entropy (0) | 2022.01.13 |
| Bilinear interpolation (0) | 2022.01.12 |


